[Programmers] 퍼즐 조각 채우기(Javascript)

I 문제 링크

---

https://programmers.co.kr/learn/courses/30/lessons/84021

코딩테스트 연습 - 퍼즐 조각 채우기

 

 

---

II 문제 풀이

---

해당 문제는 위클리 챌린지에 올라왔던 문제이고, 알고리즘 스터디에서 이번주 과제로 정했던 문제다.

비록 Level 3였지만 이런 평면과 관련된 문제는 길찾기만 해봤던 나에게 매우 도전적인 문제였다. 그냥 길찾기도 Level 3인데..

 

문제를 본 순간 떠올린 것은 다음과 같다.

1. 테이블을 순회하며 블록을 탐색한 후 기준을 (0, 0)으로 옮긴 블록들의 배열을 만든다.
2. 게임 보드에서 빈칸을 탐색하면서 블록 배열을 순회하면서 끼워 맞춰본다.
3. 안맞으면 회전시켜본다.

 

구현 상의 문제는 탐색과 회전이었다.

탐색은 어차피 블록끼리 맞닿을 일이 없어서 dfs로 하면 되겠다 싶었고, 회전이 문제였다.

 

어떻게 하면 회전을 구현할 수 있을까? 일단 그림을 그려보았다.

 

그림에는 소질이 없지만 아무튼 FE 지망중

 

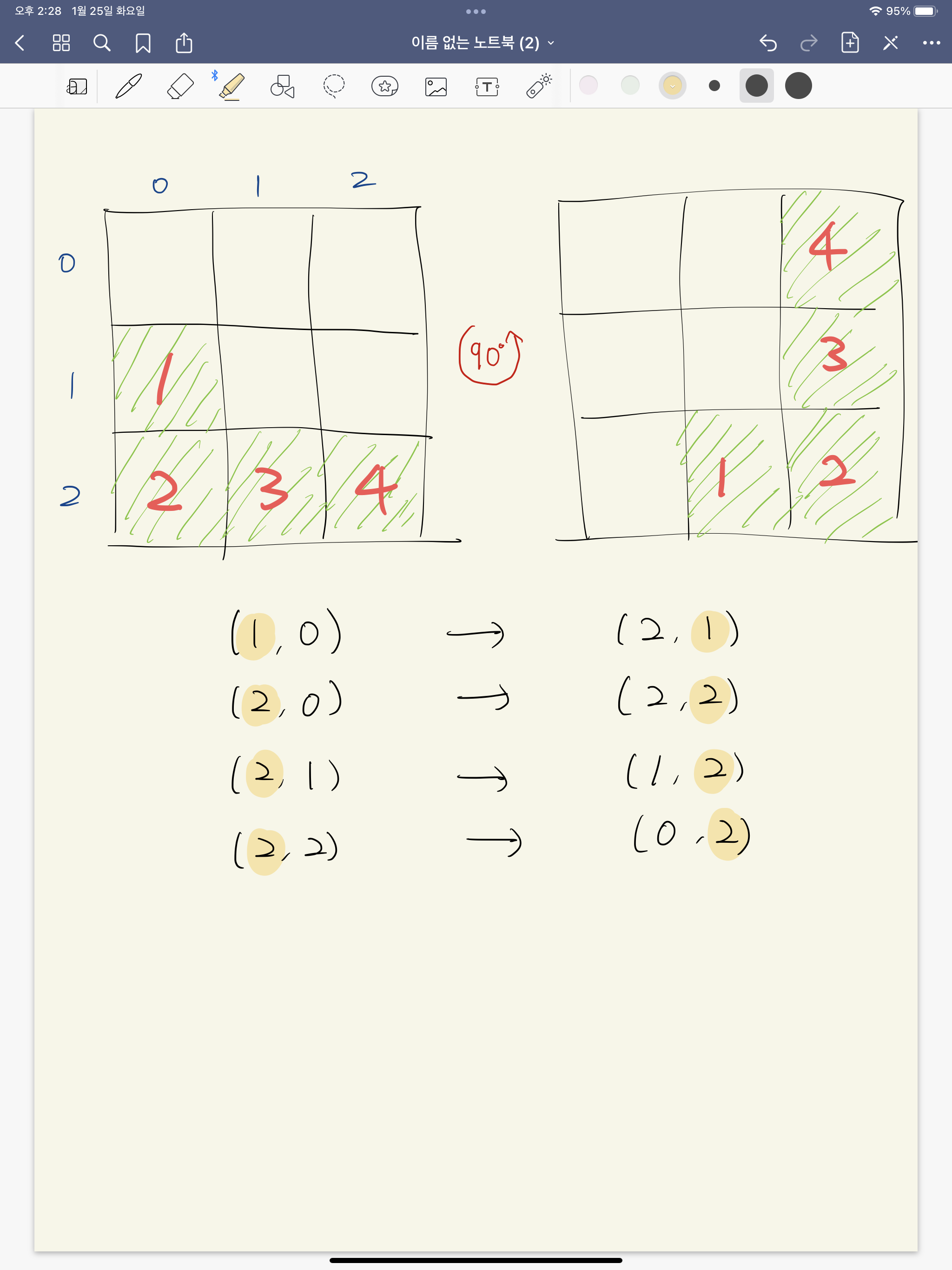
블록을 90도로 돌리는 것을 그려보았는데, 블록의 각 조각마다 대응되는 좌표를 찍어보니 규칙이 보이기 시작했다.

일단 원래의 행과 회전한 후의 열이 서로 같았다.

그리고 회전한 후 행은 원래의 열을 최대치인 2에서 뺀 값과 같았다.

말은 복잡한데, 코드로 나타내면 다음과 같다.

 

rotatedMatrix[col][size - 1 - row] = matrix[row][col];

 

그런데 나는 블록을 행렬로 관리하고 싶지 않고, 좌표의 모음으로 관리하고 싶었다.

따라서 블록을 회전시키기에는 매번 그 블록의 크기를 계산해야하므로 피곤했다.

 

그래서 다음과 같은 생각을 했다.

블록이 아니라, 게임 보드를 회전시키자

 

이러면 굉장히 잘풀리는 게, 게임 보드는 항상 정사각형에 크기가 고정이므로 위에 작성한 코드를 적용하기 매우 편하다.

따라서 블록 배열만 있다면 게임 보드를 순회(완탐)하면서 빈칸을 기준으로 블록들과 비교하면 이 블록이 들어가는 지 안들어가는 지를 판단할 수 있고, 이를 게임 보드를 한번씩 회전하면서 총 4번 돌리면 블록을 회전하면서 끼워 맞추는 것과 동일하게 할 수 있다.

 

또한 처음에는 빈칸도 블록처럼 배열로 만들어야하나 생각했는데, 블록을 (0, 0) 기준으로 어떻게 생겼는 지 저장했기 때문에 그냥 빈칸에 도착했을 때 그 지점을 기준으로 블록에 있는 좌표들을 순회하면서 비어있는 지 확인하면 됐다.

그런데 이렇게 하면 블록보다 큰 빈 칸에 블록을 집어넣는 불상사가 생긴다. 문제 조건상 이 경우는 해당이 안되기 때문에 dfs를 한번 더 돌면서 빈칸의 개수와 블록의 크기를 먼저 맞춰보는 것으로 해결했다.

 

생각을 코드로 옮기는 데에 있어서 어려운 부분이 많이 있었는데, 때마침 아이디어가 꽤 비슷한 블로그 글을 발견해서 많이 참고(특히 dfs)하게 되었다. [ https://dev-note-97.tistory.com/288 ] 다음에는 나도 커링 써봐야지..

 

그렇게 작성한 코드는 다음과 같다.

 

const BLANKED = 0;
const BLOCKED = 1;

let SIZE, GAME_BOARD, TABLE, blocks, visited;

const solution = (game_board, table) => {
  let answer = 0;
  
  SIZE = game_board.length;
  GAME_BOARD = deepCopy(game_board);
  TABLE = deepCopy(table);
  blocks = [];
  
  for (let i = 0; i < SIZE; i++) {
    for (let j = 0; j < SIZE; j++) {
      if (TABLE[i][j] === BLOCKED) {
        blocks.push(getBlock(i, j, 0, 0));
      }
    }
  }
  
  for (let rotate = 0; rotate < 4; rotate++) {
    for (let i = 0; i < SIZE; i++) {
      for (let j = 0; j < SIZE; j++) {
        if (GAME_BOARD[i][j] === BLANKED) {
          visited = deepCopy(GAME_BOARD);
          const emptySize = getEmptySize(i, j);
          for (let k = 0; k < blocks.length; k++) {
            const block = blocks[k];
            if (block.length !== emptySize) {
              continue;
            }
            if (checkFit(block, i, j)) {
              answer += block.length;
              putBoard(block, i ,j);
              blocks.splice(k, 1);
              break;
            }
          }
        }
      }
    }
    rotateBoard();
  }
  return answer;
};

const getBlock = (r, c, movedR, movedC) => {
  TABLE[r][c] = 0;
  const pieces = [{
    row: movedR,
    col: movedC
  }];
  if (r > 0 && TABLE[r - 1][c] === BLOCKED) {
    pieces.push(...getBlock(r - 1, c, movedR - 1, movedC));
  }
  if (r < SIZE - 1 && TABLE[r + 1][c] === BLOCKED) {
    pieces.push(...getBlock(r + 1, c, movedR + 1, movedC));
  }
  if (c > 0 && TABLE[r][c - 1] === BLOCKED) {
    pieces.push(...getBlock(r, c - 1, movedR, movedC - 1));
  }
  if (c < SIZE - 1 && TABLE[r][c + 1] === BLOCKED) {
    pieces.push(...getBlock(r, c + 1, movedR, movedC + 1));
  }
  return pieces;
};

const getEmptySize = (r, c) => {
  visited[r][c] = BLOCKED;
  let cnt = 1;
  if (r > 0 && visited[r - 1][c] === BLANKED) {
    cnt += getEmptySize(r - 1, c);
  }
  if (r < SIZE - 1 && visited[r + 1][c] === BLANKED) {
    cnt += getEmptySize(r + 1, c);
  }
  if (c > 0 && visited[r][c - 1] === BLANKED) {
    cnt += getEmptySize(r, c - 1);
  }
  if (c < SIZE - 1 && visited[r][c + 1] === BLANKED) {
    cnt += getEmptySize(r, c + 1);
  }

  return cnt;
};

const checkFit = (block, r, c) => block.every((piece => {
  const { row, col } = piece;
  return (r + row < SIZE) && (c + col < SIZE) && (GAME_BOARD[r + row][c + col] === BLANKED);
}));

const putBoard = (block, r, c) => {
  block.map((piece) => {
    const { row, col } = piece;
    GAME_BOARD[r + row][c + col] = BLOCKED;
  });
};

const rotateBoard = () => {
  const newBoard = deepCopy(GAME_BOARD);
  for (let r = 0; r < SIZE; r++) {
    for (let c = 0; c < SIZE; c++) {
      newBoard[c][SIZE - 1 - r] = GAME_BOARD[r][c];
    }
  }
  GAME_BOARD = newBoard;
};

const deepCopy = (matrix) => {
  const size = matrix.length;
  const newMatrix = Array.from(Array(size), () => Array(size));
  for (let i = 0; i < size; i++) {
    for (let j = 0; j < size; j++) {
      newMatrix[i][j] = matrix[i][j];
    }
  }
  return newMatrix;
};

 

III 느낀점

---

생각은 금방 했는데 코드로 선뜻 옮겨쓰는 것이 쉽지 않았다.

dfs만 할 줄 안다고 해서 금방 풀 수 있는 게 아니라 한 문제 안에 여러 가지의 센스가 필요했고, JS라서 고차함수 써가면서 했지만 이것을 C++로 한다면 매우 고통스러웠을 것이다.

 

JS에서 배열은 참조형이기 때문에 깊은 복사를 하려면 따로 작업을 해줘야 하는데, 1차원 배열은 스프레드 문법으로 가능하나 2차원 배열은 스프레드를 써도 자식 배열이 결국 참조형이기 때문에 deepCopy()를 만들어줬다. 항상 이거 때문에 한참 헤맸고, 이번에도 헤맸다..

 

알고리즘 대회가 아닌 일반적인 코테들의 마지노선이 그래프 탐색이라고 생각하는 사람으로서, 길찾기만 죽어라 푼다고 다 풀 수 있는 게 아니구나라고 느끼게 되었다. 적재적소에 어떤 알고리즘을 사용할 것인지 판단하는 것은 정말 어려운 일이다.

 

 

 

 

 

 

 

 

 

 

Coding Space by MIR :

프로그래머스 위클리 챌린지

Programmers 퍼즐 조각 채우기 Javascript

프로그래머스 퍼즐 조각 채우기 Javascript